Hình thang vuông là loại hình thang có cạnh bên bằng chiều cao của hình thang. Vậy cách tính hình thang vuông có điểm gì khác biệt so với hình thang thường? Hiểu rõ cách tính diện tích hình thang vuông giúp học sinh tự tin hơn khi đối mặt với các dạng bài tập liên quan đến hình thang vuông. Hình thang là một hình tứ giác với một cặp cạnh đối diện song song gọi là cạnh đáy, có sự khác nhau về chiều dài và các góc giữa chúng. Hình thang bao gồm nhiều loại khác nhau như hình thang thông thường, hình thang vuông, hình thang cân. Mỗi loại sẽ có đặc điểm khác nhau, từ đó cách tính chu vi, diện tích cũng sẽ có sự khác biệt đáng kể. Hình thang vuông là một trong những trường hợp đặc biệt của hình thang khi một trong hai cạnh bên của nó vuông góc với hai cạnh đáy. Điều này có nghĩa là hình thang vuông sẽ có hai góc vuông, giúp quá trình tính toán trở nên đơn giản hơn. Nhưng để thực sự nắm vững cách tính toán, học sinh cần biết công thức chung và cách áp dụng nó vào bài tập thực tế. Công thức chung để tính diện tích hình thang là trung bình cộng của chiều dài hai cạnh đáy, sau đó nhân với chiều cao. Đặc biệt với công thức tính diện tích hình thang vuông, chiều cao chính là độ dài cạnh bên vuông góc với hai đáy. Công thức tính diện tích hình thang vuông cụ thể như sau: Trong đó: Hãy lưu ý rằng các cạnh này đều phải sử dụng cùng một đơn vị đo lường. Ví dụ như các cạnh đáy và chiều cao phải cùng đơn vị là cm hoặc m. Do đó khi làm bài, học sinh phải quy đổi đơn vị sao cho thống nhất nếu thấy phần đơn vị của các cạnh khác nhau. Giả sử chúng ta có một hình thang vuông với thông số như sau: Áp dụng công thức trên thì diện tích hình thang vuông bằng: S = [(a + b) × h] / 2 = [(10 + 15) × 5] / 2 = 62.5 cm². Một điểm đặc biệt trong toán học chính là khả năng ứng dụng linh hoạt các công thức vào nhiều trường hợp khác nhau. Dưới đây là một số ví dụ cụ thể giúp học sinh mở rộng kiến thức khi tính diện tích hình thang vuông: Các bài toán yêu cầu tính diện tích khi chỉ biết độ dài cạnh bên thường yêu cầu khả năng suy luận từ các dữ kiện cho trước. Ví dụ: Một mảnh đất có dạng hình thang vuông. Cạnh bên vuông góc với hai đáy dài 6 m. Cạnh đáy lớn dài hơn cạnh đáy nhỏ 4 m. Biết rằng cạnh đáy nhỏ dài bằng 1 nửa chiều cao. Hỏi diện tích mảnh đất đó là bao nhiêu mét vuông? Hướng dẫn giải: Bước 1: Tính độ dài cạnh đáy nhỏ Vì cạnh đáy nhỏ dài bằng 1 nửa chiều cao nên cạnh đáy nhỏ = 6 : 2 = 3 (m). Bước 2: Tính độ dài cạnh đáy lớn Vì cạnh đáy lớn dài hơn cạnh đáy nhỏ 4 m nên cạnh đáy lớn = 3 + 4 = 7 (m). Bước 3: Tính diện tích hình thang vuông Áp dụng công thức tính hình thang vuông: S = [(3 + 7) × 6] / 2 = 30 m². Bài toán có thể yêu cầu tính toán khi chiều cao không phải là cạnh bên, điều này biến hình thang vuông thành một hình học phức tạp hơn. Hãy cố gắng chuyển đổi hình học ban đầu để tối giản hóa tính toán như chia hình thang thành các hình nhỏ hơn để dễ tính toán diện tích. Bài tập 1: Hãy tính diện tích của một miếng đất hình thang vuông có cạnh đáy song song dài 20 m và 25 m với chiều cao là 10 m. Lời giải: S = (20 + 25) × 10 / 2 = 225 m². Bài tập 2: Một cái hồ bơi hình thang vuông có đáy lớn là 30 m, đáy nhỏ là 20 m và chiều cao là 12 m. Hãy tính diện tích của hồ bơi. Lời giải: S = (30 + 20) × 12 / 2 = 300 m². Để tối ưu hóa việc tính diện tích hình thang vuông, học sinh nên lưu ý những điều sau: Những phương pháp này không chỉ mang lại sự chính xác mà còn rèn luyện khả năng tư duy logic và sáng tạo cho học sinh. Với những công thức và phương pháp trên, hy vọng bạn đã biết cách tính diện tích hình thang vuông một cách dễ dàng. Chúc bạn học tập hiệu quả và gặt hái nhiều thành công! Bạn đang tìm kiếm người bạn đồng hành lý tưởng cho cả học tập, giải trí? Đừng bỏ lỡ cơ hội sở hữu laptop học sinh - sinh viên tại FPT Shop! Khám phá ngay hôm nay để tận hưởng những chương trình khuyến mãi hấp dẫn và lựa chọn chiếc laptop phù hợp nhất với phong cách của bạn! Laptop sinh viên Xem thêm:Hiểu về hình thang và hình thang vuông
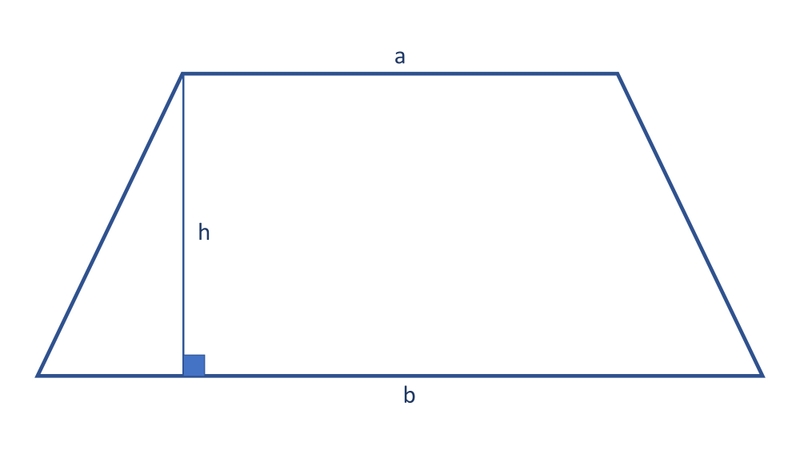
Công thức tính diện tích hình thang vuông
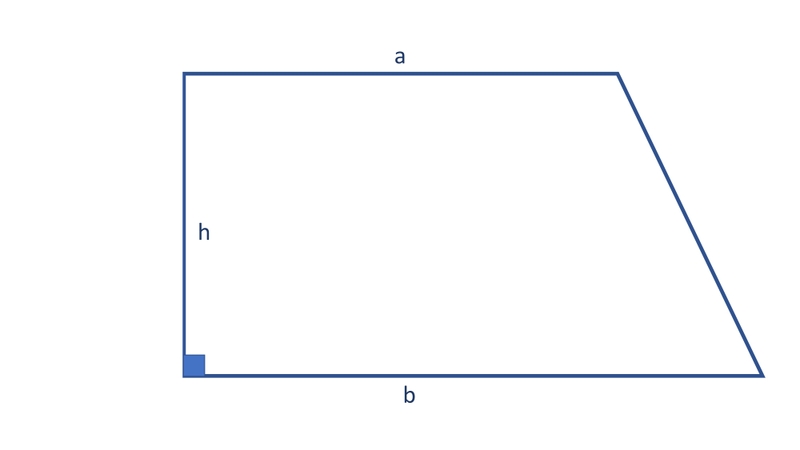
Ví dụ minh họa cách tính diện tích hình thang vuông
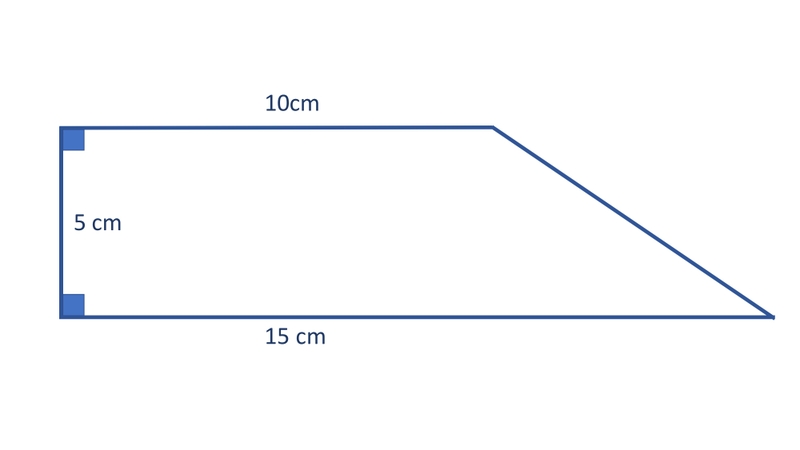
Hướng dẫn một số cách giải bài toán hình thang
Tính diện tích khi chỉ biết độ dài cạnh bên
Ví dụ 2: Tính diện tích với điều kiện bất đối xứng
Bài tập ứng dụng thực tiễn
Mẹo và lưu ý khi tính diện tích hình thang vuông
Tạm kết
Hướng dẫn cách tính diện tích hình thang vuông một cách chi tiết và dễ hiểu







Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm