Lý thuyết một số hệ thức về cạnh và đường cao trong tam giác vuông | SGK Toán lớp 9



Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
1. Hệ thức về cạnh và đường cao trong tam giác vuông
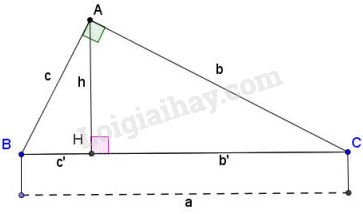
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) (hình vẽ). Khi đó ta có các hệ thức sau:

+) \(A{B^2} = BH.BC\) và \(A{C^2} = CH.BC\) hay \({c^2} = a.c'\) và \({b^2} = ab'\) (1)
+) \(H{A^2} = HB.HC\) hay \({h^2} = c'b'\) (2)
+) \(AB.AC = BC.AH\) hay \(cb = ah\) (3)
+) \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\) hay \(\dfrac{1}{{{h^2}}} = \dfrac{1}{{{c^2}}} + \dfrac{1}{{{b^2}}}\) (4).
+) \(B{C^2} = A{B^2} + A{C^2}\) (Định lí Pitago).
2. Các dạng toán cơ bản
Dạng 1: Tính độ dài các đoạn thẳng trong tam giác vuông
Phương pháp:
Sử dụng hệ thức về cạnh và đường cao trong tam giác vuông.
Dạng 2: Chứng minh các hệ thức liên quan giữa các yếu tố trong tam giác vuông
Phương pháp:
Ta thường sử dụng các kiến thức:
- Đưa về hai tam giác đồng dạng có chứa các đoạn thẳng có trong hệ thức.
- Sử dụng các hệ thức về cạnh và đường cao trong tam giác vuông để chứng minh.

Loigiaihay.com