Công Thức Tính Chu Vi Hình Thoi Và Các Ứng Dụng Thực Tế

Mô tả sản phẩm

Giới Thiệu Về Hình Thoi

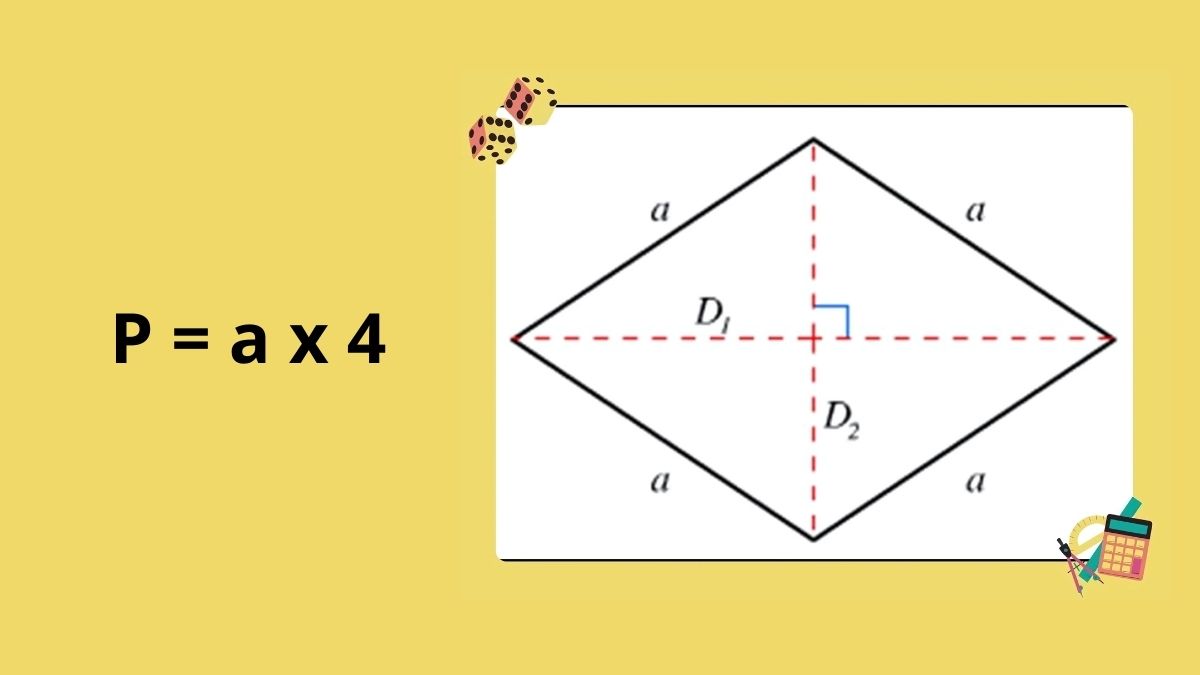
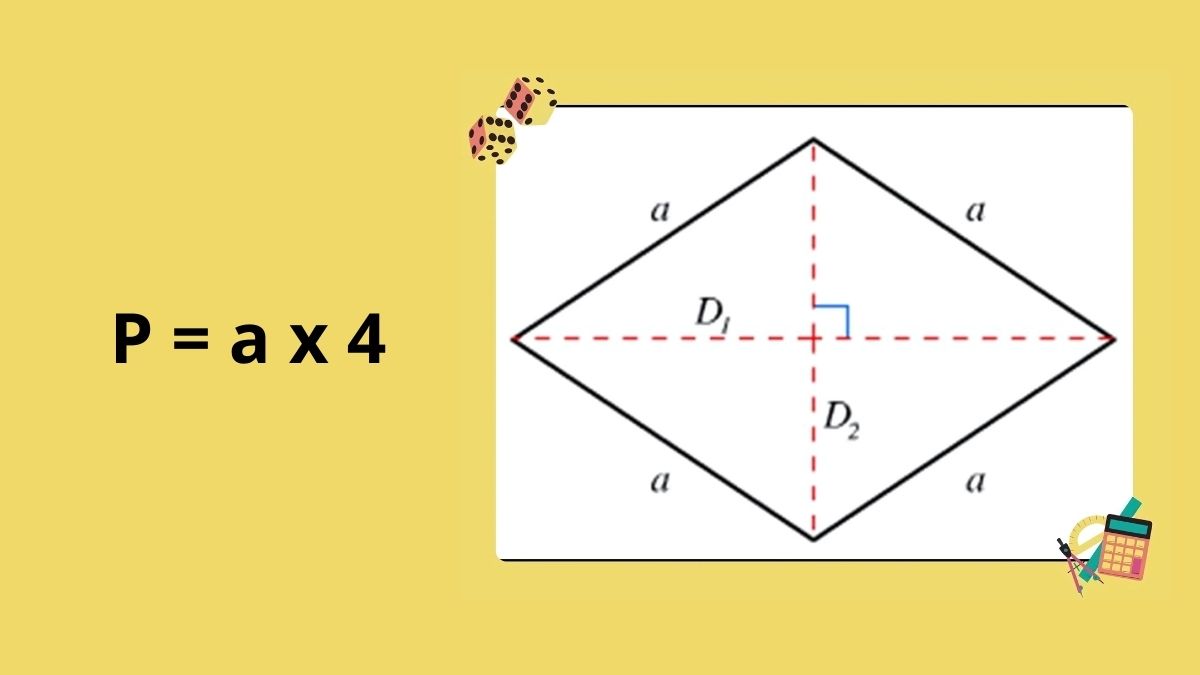
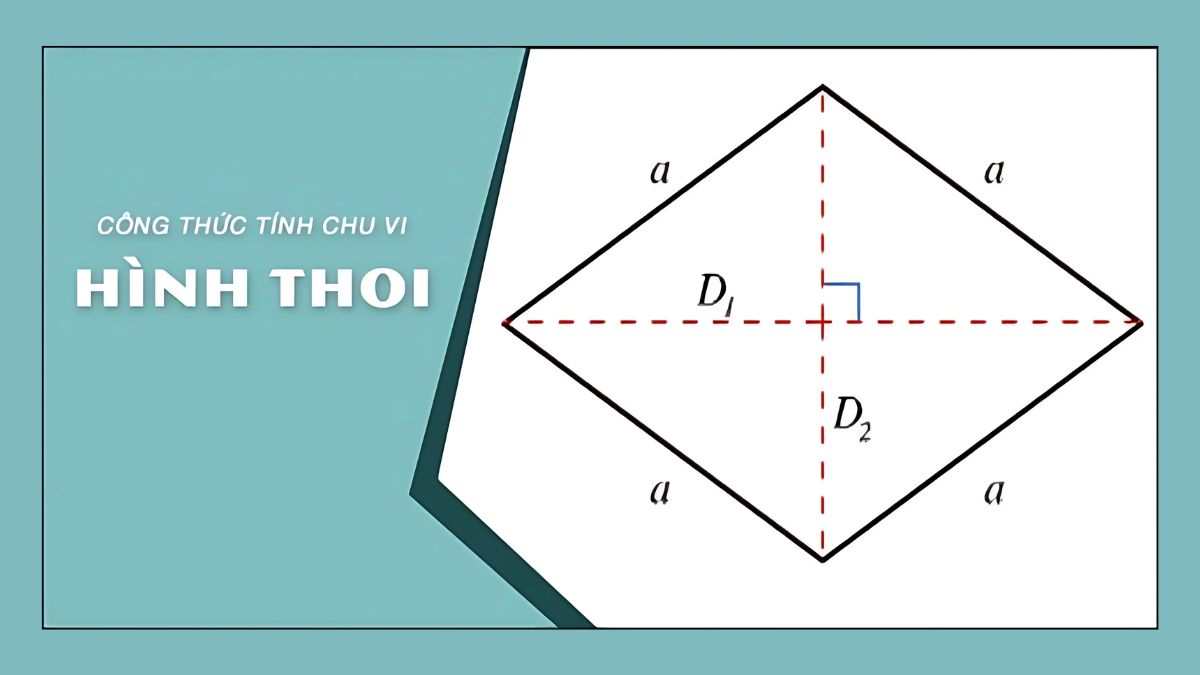
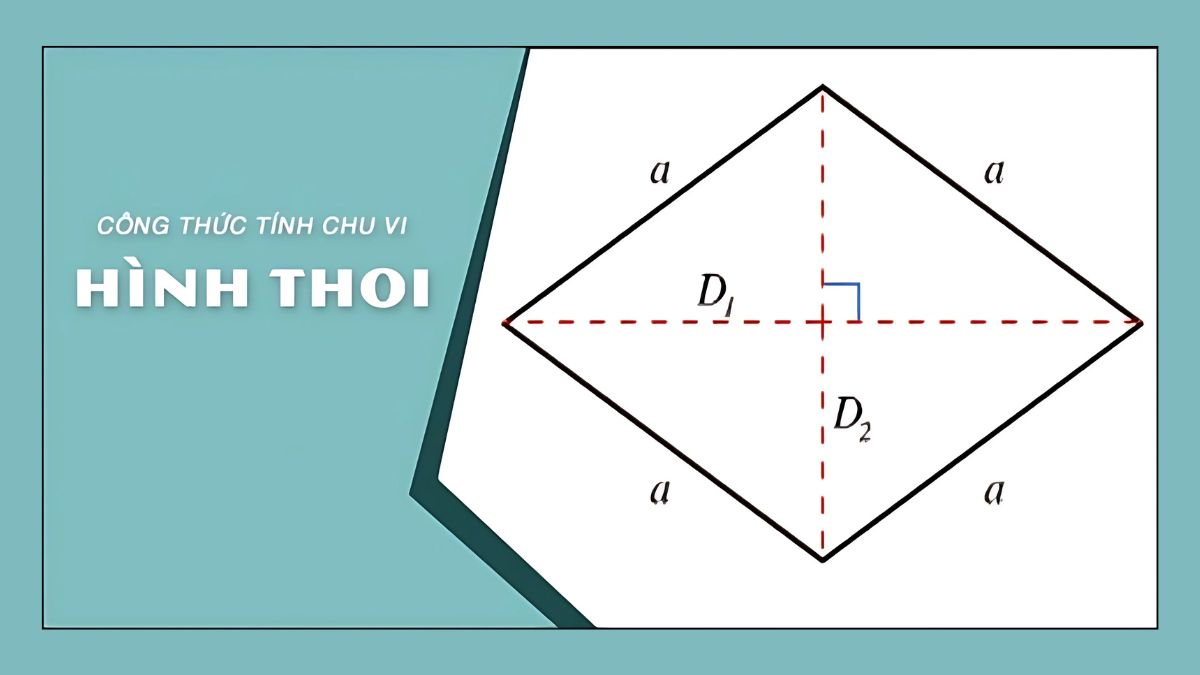
Hình thoi là một tứ giác có bốn cạnh bằng nhau và là một dạng đặc biệt của hình bình hành. Ngoài việc có các cạnh bằng nhau, hình thoi còn có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường. Hình thoi cũng có các góc đối bằng nhau, tạo nên những tính chất hình học thú vị. Trong bài viết này, chúng ta sẽ tập trung vào công thức tính chu vi hình thoi và các ứng dụng thực tế của nó.

Công Thức Tính Chu Vi Hình Thoi

Chu vi hình thoi được tính bằng tổng độ dài của bốn cạnh. Vì tất cả các cạnh của hình thoi đều bằng nhau nên công thức tính chu vi rất đơn giản:

Chu vi (P) = 4 × a

Trong đó:
- a là độ dài một cạnh của hình thoi.

Ví dụ, nếu một cạnh của hình thoi có độ dài 5 cm, chu vi của hình thoi đó sẽ là:

P = 4 × 5 = 20 cm.

Cách Tính Chu Vi Khi Biết Đường Chéo

Trong một số trường hợp, bạn có thể biết độ dài hai đường chéo của hình thoi nhưng không biết độ dài cạnh. Khi đó, bạn có thể sử dụng định lý Pythagoras để tìm độ dài cạnh trước khi tính chu vi.

Giả sử:
- d1 và d2 là độ dài hai đường chéo.

Vì hai đường chéo cắt nhau tại trung điểm và vuông góc với nhau, mỗi nửa đường chéo sẽ tạo thành một tam giác vuông với cạnh của hình thoi. Do đó, độ dài cạnh a có thể tính bằng:

a = √((d1/2)² + (d2/2)²)

Sau khi tìm được a, bạn có thể áp dụng công thức chu vi như trên.

Ứng Dụng Thực Tế Của Hình Thoi

Hình thoi không chỉ là một khái niệm hình học mà còn có nhiều ứng dụng trong đời sống và các ngành nghề khác nhau:

- Kiến trúc và xây dựng: Hình thoi được sử dụng trong thiết kế các mẫu gạch lát sàn, cửa sổ trang trí, hoặc các họa tiết trên tường.
- Thời trang: Nhiều mẫu trang sức, túi xách, hoặc họa tiết trên quần áo sử dụng hình thoi để tạo sự cân đối và hài hòa.
- Công nghệ: Trong các bảng mạch điện tử, hình thoi có thể được dùng để thiết kế các linh kiện hoặc mạch in.

Bài Tập Thực Hành

Để củng cố kiến thức, hãy thử giải các bài tập sau:

1. Một hình thoi có cạnh dài 8 cm. Tính chu vi của nó.
2. Một hình thoi có hai đường chéo lần lượt là 6 cm và 8 cm. Tính chu vi của hình thoi này.

Đáp án:
1. P = 4 × 8 = 32 cm.
2. a = √((6/2)² + (8/2)²) = √(9 + 16) = 5 cm → P = 4 × 5 = 20 cm.

Kết Luận

Tính chu vi hình thoi là một bài toán đơn giản nhưng quan trọng trong hình học. Bằng cách nắm vững công thức và hiểu rõ các tính chất của hình thoi, bạn có thể dễ dàng áp dụng vào nhiều tình huống thực tế khác nhau. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách tính chu vi hình thoi và các ứng dụng của nó.

Xem thêm: công thức hình học không gian lớp 9