Công thức tính khoảng cách từ điểm đến mặt phẳng trong không gian

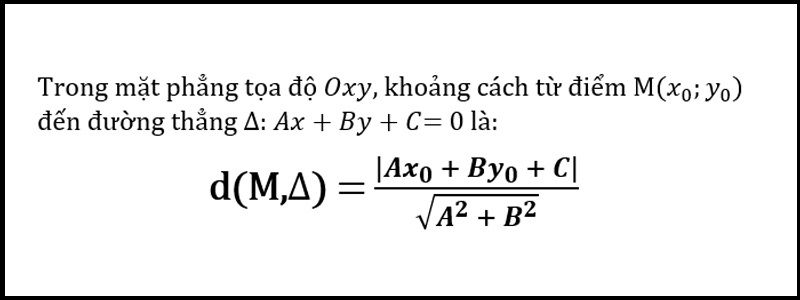
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
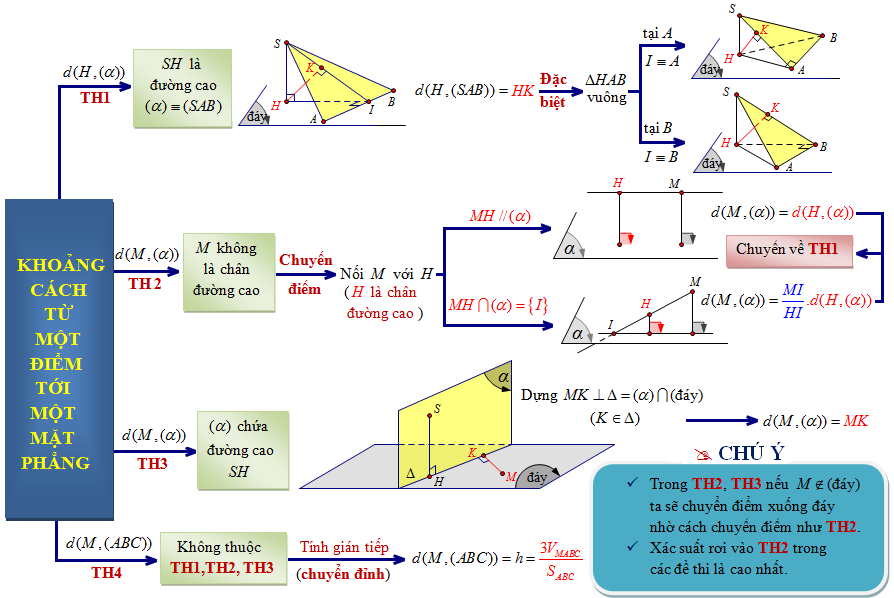
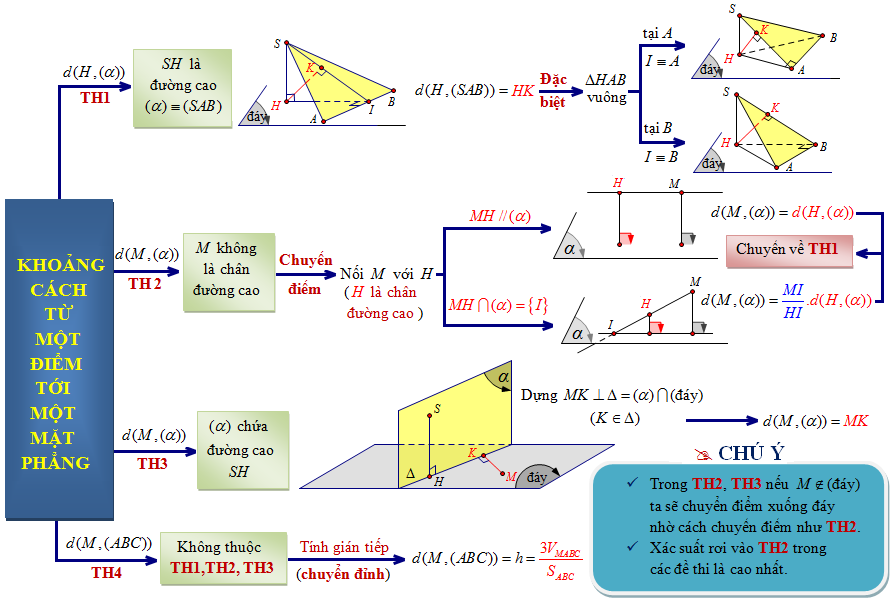
Giới thiệu về khoảng cách từ điểm đến mặt phẳng
Trong hình học không gian, việc xác định khoảng cách từ một điểm đến một mặt phẳng là bài toán cơ bản nhưng có nhiều ứng dụng quan trọng. Khoảng cách này được sử dụng rộng rãi trong các lĩnh vực như đồ họa máy tính, xây dựng, vật lý và nhiều ngành khoa học khác. Bài viết này sẽ cung cấp cho bạn công thức tính khoảng cách từ điểm đến mặt phẳng một cách chi tiết và dễ hiểu.Công thức tổng quát tính khoảng cách từ điểm đến mặt phẳng
Cho mặt phẳng (P) có phương trình tổng quát: Ax + By + Cz + D = 0 và điểm M(x₀, y₀, z₀). Khoảng cách từ điểm M đến mặt phẳng (P) được tính bằng công thức:d(M, (P)) = |Ax₀ + By₀ + Cz₀ + D| / √(A² + B² + C²)
Trong đó:
- A, B, C là các hệ số của phương trình mặt phẳng
- D là hằng số trong phương trình mặt phẳng
- (x₀, y₀, z₀) là tọa độ của điểm M
Chứng minh công thức tính khoảng cách
Để chứng minh công thức này, ta có thể sử dụng phương pháp hình chiếu. Giả sử N là hình chiếu vuông góc của M lên mặt phẳng (P). Khoảng cách từ M đến (P) chính là độ dài đoạn MN. Vector pháp tuyến của mặt phẳng (P) là n→ = (A, B, C). Ta có thể tính MN bằng cách chiếu vector NM→ lên vector pháp tuyến n→.Ví dụ minh họa cách tính khoảng cách
Xét mặt phẳng (P): 2x - 3y + 6z - 12 = 0 và điểm M(1, 2, 3). Áp dụng công thức:d = |2*1 + (-3)*2 + 6*3 - 12| / √(2² + (-3)² + 6²) = |2 - 6 + 18 - 12| / √(4 + 9 + 36) = |2| / √49 = 2/7
Vậy khoảng cách từ M đến (P) là 2/7 đơn vị độ dài.
Trường hợp đặc biệt khi mặt phẳng đi qua gốc tọa độ
Khi mặt phẳng đi qua gốc tọa độ (D = 0), công thức trở thành:d = |Ax₀ + By₀ + Cz₀| / √(A² + B² + C²)
Ví dụ: Cho mặt phẳng (P): x + 2y - 2z = 0 và điểm M(1, 1, 1). Khoảng cách là:
d = |1*1 + 2*1 - 2*1| / √(1 + 4 + 4) = |1| / 3 = 1/3
Ứng dụng của công thức trong thực tế
Công thức này có nhiều ứng dụng thực tế:- Trong kiến trúc: tính khoảng cách từ một điểm đến bề mặt tường, sàn nhà
- Trong đồ họa máy tính: xác định khoảng cách từ camera đến các đối tượng 3D
- Trong vật lý: tính khoảng cách từ một hạt đến mặt phẳng phân cách giữa hai môi trường
- Trong robot: lập trình đường di chuyển tránh vật cản
Các lưu ý khi sử dụng công thức
Khi áp dụng công thức, cần chú ý:- Phương trình mặt phẳng phải ở dạng chuẩn Ax + By + Cz + D = 0
- Nếu phương trình mặt phẳng chưa ở dạng chuẩn, cần biến đổi về dạng chuẩn trước khi tính toán
- Kết quả khoảng cách luôn là giá trị không âm
- Công thức chỉ áp dụng cho không gian 3 chiều
Mở rộng: Khoảng cách từ điểm đến mặt phẳng trong không gian n chiều
Trong không gian n chiều, mặt phẳng được gọi là siêu phẳng (hyperplane) có phương trình tổng quát a₁x₁ + a₂x₂ + ... + aₙxₙ + b = 0. Khoảng cách từ điểm P(p₁, p₂, ..., pₙ) đến siêu phẳng được tính bằng:d = |a₁p₁ + a₂p₂ + ... + aₙpₙ + b| / √(a₁² + a₂² + ... + aₙ²)
Kết luận
Công thức tính khoảng cách từ điểm đến mặt phẳng là một công cụ mạnh mẽ trong hình học không gian. Hiểu và vận dụng thành thạo công thức này sẽ giúp bạn giải quyết nhiều bài toán thực tế trong học tập và công việc. Hãy luyện tập với nhiều ví dụ khác nhau để nắm vững cách áp dụng công thức này trong các tình huống cụ thể.Xem thêm: ốc đào trường sa