:quality(75)/r_la_tap_hop_so_gi_a4e08ba962.png)
R là tập hợp số gì? Đây là câu hỏi cơ bản nhưng vô cùng quan trọng trong chương trình Toán học THCS và THPT. Tập hợp R đại diện cho tập hợp số thực bao gồm số nguyên, phân số, thập phân và số vô tỉ. Việc nắm vững khái niệm này giúp bạn dễ dàng xử lý các bài toán từ đơn giản đến nâng cao.
R là tập hợp số gì? Nếu bạn từng gặp ký hiệu ℝ trong các bài toán thì R là ký hiệu của tập hợp số thực - một tập hợp nền tảng trong đại số. Số thực bao gồm mọi số có thể biểu diễn trên trục số, từ số nguyên đến số thập phân vô hạn không tuần hoàn. R là tập hợp số gì? Trong toán học, ký hiệu R (hoặc ℝ) đại diện cho tập hợp số thực (Real numbers). Đây là một trong những khái niệm cơ bản và quan trọng nhất trong toán học, được sử dụng rộng rãi từ cấp trung học đến đại học và nghiên cứu khoa học. Tập hợp số thực R là tập hợp bao gồm tất cả các số có thể biểu diễn trên trục số, gồm: Để hiểu rõ R là tập hợp số gì cũng như vị trí của R, ta cần xem xét cấu trúc phân cấp: Trong đó: Xét các số sau và xác định chúng thuộc tập con nào của R: a) 3 → Thuộc N, Z, Q, R b) -4 → Thuộc Z, Q, R (không thuộc N) c) 1/2 → Thuộc Q, R (không thuộc N, Z) d) √2 ≈ 1.414... → Chỉ thuộc R (số vô tỷ) e) π ≈ 3.14159... → Chỉ thuộc R (số vô tỷ) Trên trục số thực, ta có thể biểu diễn: Quan hệ thứ tự Xác định các số sau thuộc tập con nào của R: a) -7 b) 3/4 c) √9 d) √5 e) 0.333... f) π/2 Đáp án: a) -7 ∈ Z, Q, R b) 3/4 ∈ Q, R c) √9 = 3 ∈ N, Z, Q, R d) √5 ∈ R (số vô tỷ) e) 0.333... = 1/3 ∈ Q, R f) π/2 ∈ R (số vô tỷ) Viết các tập hợp sau dưới dạng khoảng: a) {x ∈ R | -2 < x ≤ 5} b) {x ∈ R | x ≥ 3} c) {x ∈ R | |x| < 4} Đáp án: a) (-2, 5] b) [3, +∞) c) (-4, 4) Chứng minh rằng giữa hai số thực phân biệt a và b (a < b) luôn tồn tại một số thực c sao cho a < c < b. Lời giải: Chọn c = (a + b)/2. Ta có: c - a = (a + b)/2 - a = (b - a)/2 > 0 (vì b > a) b - c = b - (a + b)/2 = (b - a)/2 > 0 (vì b > a) Vậy a < c < b. Một chiếc xe chạy với vận tốc v (km/h) trong thời gian t (giờ). Quãng đường s (km) được tính theo công thức s = vt. a) Nếu v = 60 km/h và t = 2.5 giờ, tính quãng đường đi được. b) Tập hợp các giá trị có thể của v, t, s thuộc tập nào? Đáp án: a) s = 60 × 2.5 = 150 km b) Trong thực tế, v, t, s ∈ R⁺ (tập số thực dương) Tập hợp số thực R là nền tảng của toán học hiện đại, cung cấp một hệ thống số hoàn chỉnh để mô tả và tính toán các hiện tượng trong tự nhiên và xã hội. Việc hiểu rõ R là tập hợp số gì không chỉ giúp học sinh nắm vững kiến thức toán học mà còn phát triển tư duy logic và khả năng giải quyết vấn đề trong nhiều lĩnh vực khác nhau. Việc học Toán sẽ trở nên trực quan và sinh động hơn nếu bạn có một thiết bị hỗ trợ tốt. Những chiếc máy tính bảng chính hãng tại FPT Shop với màn hình lớn, hỗ trợ bút cảm ứng giúp bạn dễ dàng học, vẽ đồ thị và giải bài tập mọi lúc mọi nơi. Máy tính bảng Xem thêm:R là tập hợp số gì?
Tìm hiểu về ký hiệu R
Cấu trúc phân cấp của các tập hợp số
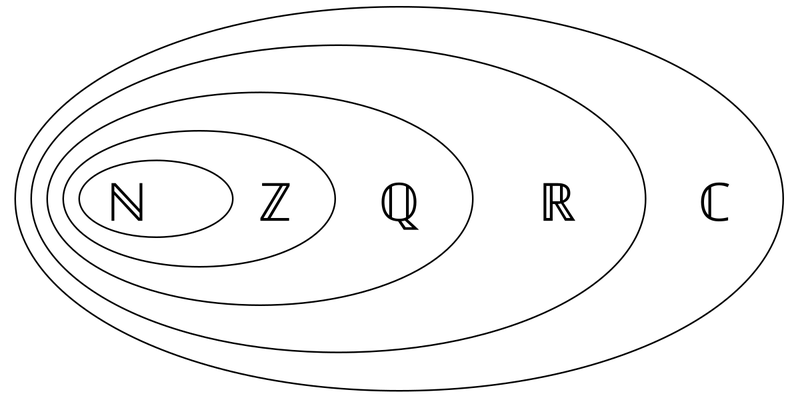
Đặc điểm của tập hợp số thực R
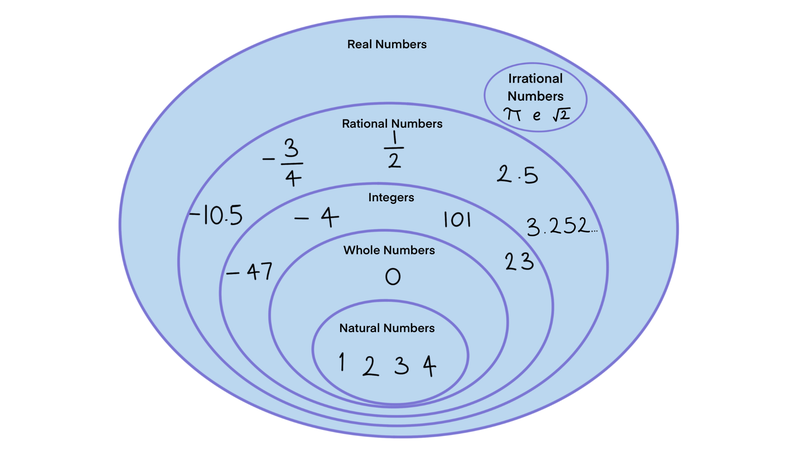
Ví dụ minh họa
Ví dụ 1: Phân loại các số thuộc R
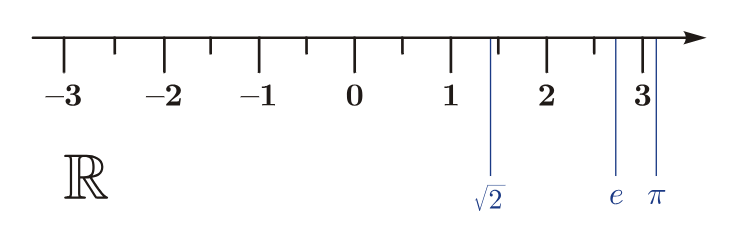
Ví dụ 2: Biểu diễn trên trục số
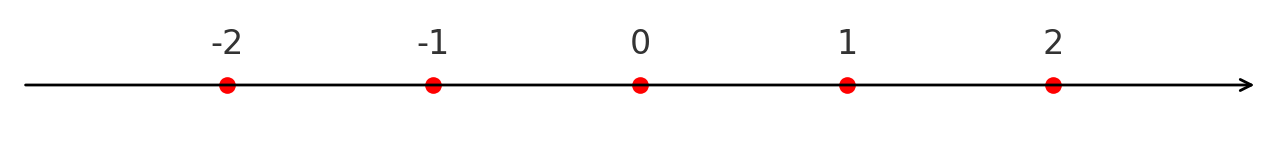
Ví dụ 3: Khoảng và đoạn trong R
Các phép toán trong R
Phép cộng và nhân
Bài tập thực hành
Bài tập 1: Phân loại số
Bài tập 2: Khoảng và đoạn
Bài tập 3: Tính chất của R
Bài tập 4: Ứng dụng thực tế

Tạm kết
