Tứ diện đều đã trở thành một biểu tượng của sự đối xứng và hoàn hảo. Với cấu trúc độc đáo được tạo nên từ bốn mặt là những tam giác đều bằng nhau, đây là khối đa diện đơn giản nhất nhưng cũng ẩn chứa nhiều tính chất toán học vô cùng thú vị. Hãy cùng FPT Shop khám phá chi tiết về hình khối đặc biệt này qua bài viết dưới đây. Trong lĩnh vực hình học, tứ diện là một trong những hình đa diện cơ bản nhưng lại chứa đựng nhiều tính chất hấp dẫn. Một tứ diện có bốn mặt, tất cả đều là tam giác, sáu cạnh và bốn đỉnh. Đây là loại hình học không gian đơn giản nhưng lại có cấu trúc rất phong phú. Tứ diện được phân thành nhiều loại khác nhau, trong đó, tứ diện đều là một ví dụ điển hình. Trong tứ diện đều, tất cả các mặt đều là tam giác đều và tất cả các cạnh đều có độ dài bằng nhau. Sự đồng nhất này tạo ra hình học không gian có tính đối xứng cao, giúp nó trở thành một đối tượng nghiên cứu quan trọng trong toán học. Tính đối xứng của tứ diện đều không chỉ làm cho nó trở nên đẹp mắt mà còn tạo ra nhiều ứng dụng thú vị trong nhiều lĩnh vực khác nhau. Ví dụ, trong lĩnh vực vật lý, tứ diện đều được sử dụng để mô tả cấu trúc của một số phân tử. Trong toán học, nó là một ví dụ điển hình cho các nghiên cứu về hình học không gian và đại số. Bên cạnh đó, tứ diện cũng có thể được sử dụng trong thiết kế và kiến trúc, nơi tính đối xứng và sự đơn giản của nó được đánh giá cao. Trong nghệ thuật, tứ diện được sử dụng để tạo ra các tác phẩm có tính đối xứng và cân đối, mang lại cảm giác thẩm mỹ và sự hài hòa. Đây là đặc điểm nổi bật và giá trị nhất của tứ diện đều. Tứ diện đều tạo ra các góc có số đo không đổi, là chìa khóa để giải quyết nhiều bài toán. Cách vẽ hình tứ diện đều sẽ trở nên thật đơn giản khi bạn nắm vững quy tắc biểu diễn không gian trên mặt phẳng. Chỉ với 3 bước logic dưới đây, bạn sẽ dễ dàng phác họa một khối tứ diện trực quan và chính xác. Để tạo cảm giác về chiều sâu, bạn hãy bắt đầu bằng cách vẽ một tam giác (ví dụ, tam giác BCD) trông như đang nằm trên một mặt phẳng. Đây chính là mặt đáy của tứ diện. Ba cạnh BC, CD và DB sẽ là các cạnh đáy của hình. Bây giờ, hãy chọn một điểm duy nhất không thuộc mặt phẳng chứa tam giác vừa vẽ (thường là chấm một điểm A ở phía trên mặt đáy). Điểm A này sẽ là đỉnh thứ tư cũng là đỉnh chính của hình chóp, quyết định chiều cao và hình dáng tổng thể của tứ diện. Cuối cùng, bạn hãy dùng thước kẻ để nối đỉnh A với ba đỉnh của mặt đáy (A nối với B, A nối với C, A nối với D). - Lưu ý quan trọng: Những cạnh nào bị các mặt khác che khuất (cạnh không nhìn thấy được từ góc nhìn của bạn), hãy biểu diễn chúng bằng nét đứt. Những cạnh nhìn thấy rõ, hãy vẽ bằng nét liền. Thao tác này sẽ tạo ra các mặt tam giác còn lại và hoàn thiện một khối tứ diện 3D trực quan. Cho tứ diện ABCD có độ dài các cạnh lần lượt là BC = a, AC = b, AB = c, AD = d, BD = e, CD = f và thể tích tứ diện là V. Qua những phân tích trên, hy vọng rằng khối tứ diện đều đã trở nên gần gũi và không còn là một khái niệm xa lạ. Việc ghi nhớ các đặc điểm và công thức quan trọng của nó sẽ là công cụ đắc lực, giúp bạn tự tin xử lý các dạng bài tập và thêm yêu thích môn hình học không gian. Để việc học tập và khám phá các mô hình không gian trở nên trực quan hơn, một chiếc máy tính bảng Lenovo chính là công cụ hỗ trợ đắc lực. Hãy tham khảo ngay các mẫu máy tính bảng Lenovo chính hãng tại FPT Shop với hiệu năng mạnh mẽ, màn hình sắc nét và nhiều ưu đãi hấp dẫn dành riêng cho học sinh, sinh viên! Xem thêm:Giới thiệu đôi nét về tứ diện


Những đặc điểm của hình tứ diện đều
Tính chất đối xứng hoàn hảo

Các góc đặc biệt (Quan trọng trong tính toán)

Chiều cao và các tâm đặc biệt

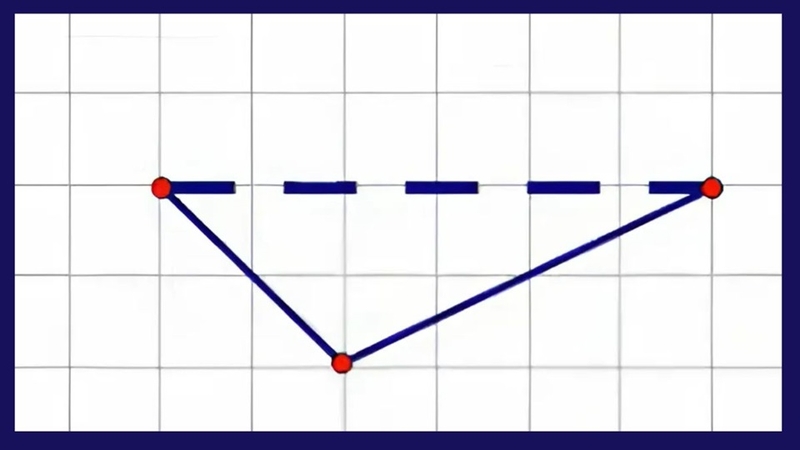
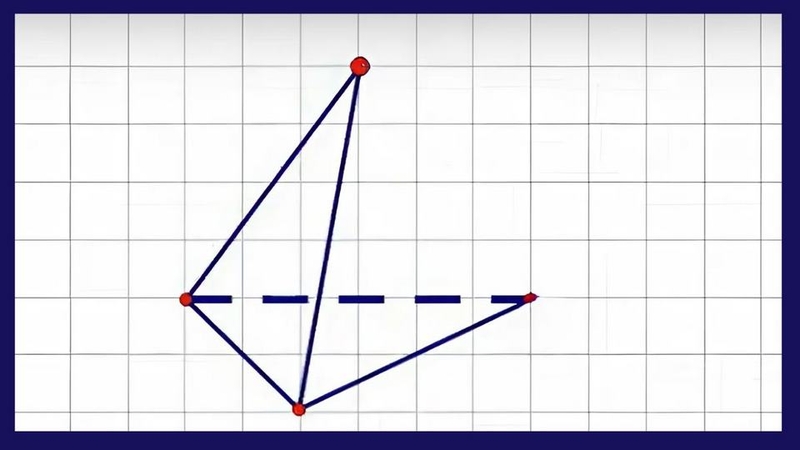
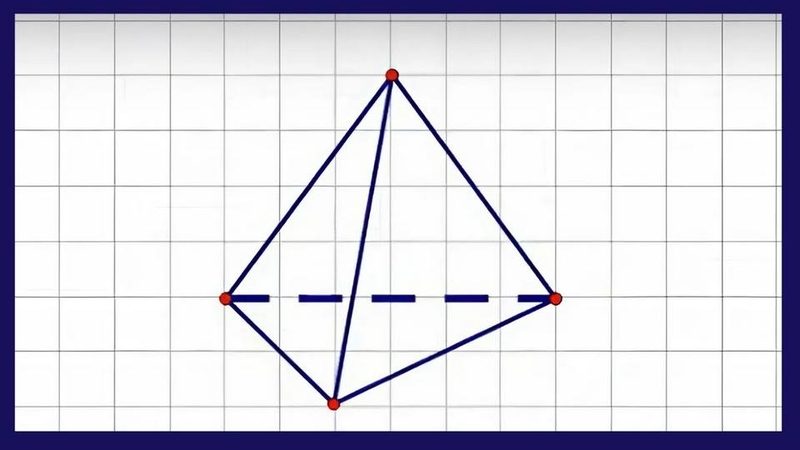
Cách vẽ hình tứ diện đều chi tiết
Những công thức tính liên quan đến hình tứ diện đều
Đối với hình tứ diện

Đối với hình tứ diện đều
Tạm kết
Tứ diện đều – Tổng hợp toàn bộ định nghĩa, đặc điểm và công thức bạn cần biết để làm toán hiệu quả












Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm